Airplane crashes make dramatic headlines every year. The two fatal crashes in 2018 and 2019 involving the Boeing 737 MAX raised concerns about airworthiness. In 2022 alone, more than 200 fatalities have been reported involving commercial flights.

In the United States, aircraft is certified for airworthiness and safety by the Federal Aviation Administration (FAA), which depends on a detailed testing campaign. Flight and engine testing for certification represent a substantial cost to airplane and engine development programs. Furthermore, the dependence on suitable weather conditions and the availability of testing facilities causes long schedule delays, costing more to the manufacturer. Certification by Analysis (CbA) is an emerging paradigm in the aerospace community. CbA aims to make aircraft (and engine) certification and qualification faster and cost-effective via the use of advanced numerical simulations and design methods with quantifiable accuracy. The ability to accurately and reliably simulate extreme flight maneuvers can dramatically reduce the amount of testing needed to be conducted by the FAA for certification. This not only reduces cost for certification but also provides uncertainty estimates of key certification metrics that allow for more reliable assessments of system safety.

Estimating the probability of failure in aerospace subsystems, which is part of the certification process, remains a challenging task. For example, the popular Monte Carlo sampling methods are intractable when costly high-fidelity simulations must be queried. Computational methods that use coarse-grained mesh resolutions and fewer solver iterations reduce the computational cost, but at a loss of accuracy. How can one meet the rigorous quantification requirements for flight certification while addressing the cost-accuracy trade-off?

To answer this question, researchers from the University of Utah, Florida State University and Argonne National Laboratory have developed a surrogate modeling approach called CAMERA – an acronym for cost-aware, adaptive, multifidelity, efficient reliability analysis. CAMERA is based on Gaussian process models that can learn the correlations between different fidelities – continuous or discrete – and predict the high-fidelity function with potentially fewer queries to the expensive high-fidelity model, supplemented by cheaper low-fidelity model queries.

“Instead of using direct Monte Carlo, we adaptively build a multifidelity surrogate model so that only the most useful fidelities and inputs are queried,” said Vishwas Rao, an assistant computational mathematician in the Mathematics and Computer Science division at Argonne National Laboratory

Adaptivity Is Key

Adaptively constructing the surrogate model involves a couple of steps. The researchers start with a seed sample, based on observations of the quantities of interest. The surrogate model built off the seed samples is then used to construct an ​“acquisition principle’’ that allows for the selection of the best next sample, according to the surrogate model, by solving an optimization problem. The acquisition principle is tailored to reduce uncertainty in the prediction of the failure boundary; in this way, sequentially repeating this process produces increasingly accurate predictions of the failure boundary.

“A highlight of our acquisition principle is that it seamlessly applies to single fidelity (when there is one model of our system) as well as multifidelity settings,” said Aswin Ranganathan, an assistant professor in the Department of Mechanical Engineering at the University of Utah. ​“Furthermore, the fidelity space can be discrete or continuous. This way, our proposed methodology finds potential applications outside of just estimating failure probabilities, for example, emulation and global optimization.”

Using surrogate models for failure probability estimation is not new. But most of the existing approaches do not actively train the surrogate model. With CAMERA, the appropriate control parameter and fidelity level to query at each step of the model building process is adaptively chosen by optimizing the acquisition function. The use of multifidelity Gaussian process models for failure probability estimation is also not new. However, existing approaches depend on learning the discrepancy between models at each fidelity level and the highest fidelity model; this necessitates querying every fidelity level at a structured grid of control parameters. Such an approach becomes intractable beyond just a handful number of fidelity levels. However, CAMERA learns the correlation between fidelity levels from a handful of scattered observations across the joint input-fidelity space. In this way, CAMERA naturally extends to continuous fidelity spaces as well.

Testing for Accuracy and Cost

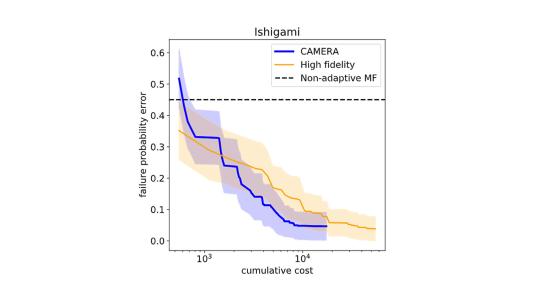
The researchers evaluated their model on four synthetic test cases and two real-world applications. For the synthetic cases, they ran single- and multifidelity experiments for 100 iterations with 20 repetitions containing randomized seed samples. In all four cases the multifidelity approach predicts the failure volume with greater accuracy than that of the single-fidelity approach (see Fig. 1).

“We also wanted to see how CAMERA balances the trade-off between accuracy and cost across the fidelity space,” Rao said. ​“We found that when there is a correlation between the low- and high-fidelity models, the algorithm exploits this feature to obtain most of its samples from the lowest-fidelity model – thus saving computational cost” (see Fig. 2).

The two real-world applications – a gas turbine blade at steady-state operating conditions and an ONERA transonic wing – showed results similar to those of the synthetic tests, including high accuracy in failure probability error, with the multifidelity approach significantly outperforming using the single expensive high-fidelity model.

CAMERA marks an important step in leveraging high-performance computing and high-fidelity models for failure probability estimation in CbA. The framework extends several existing single-fidelity acquisition functions in reliability analysis to the multifidelity setting, and the synthetic test functions can be leveraged to benchmark multifidelity methods in general. The researchers next plan to explore ideas on two fronts: more reductions in the overall computational cost and in the variance of the failure probability estimators. The overall method is implemented in PyTorch, and the researchers plan to release the software for public use in the near future.

For the full paper on this research, see S. Ashwin Renganathan, Vishwas Rao, and Ionel M. Navon, ​“CAMERA: A method for cost-aware, adaptive, multifidelity, efficient reliability analysis,” Journal of Computational Physics 472 (2023) 11698.